理解LDA算法

Latent Dirichlet Allocation（LDA）算法是一种文本挖掘算法，尤其适合从长文本中提取主题。

简而言之，LDA假设每个文档定义了一个主题（topic）的概率分布，而每个主题定义了一个词（word）的概率分布。

它还假定，文档中的每个词是这样被产生的：先从文档中抽出一个主题（比如【金融】），然后再从主题中抽出一个词（比如【货币】）。每个词的产生过程彼此独立。

LDA算法有训练和测试两个阶段 —— 训练时，输入许多文档，输出这两个概率分布的参数；测试时，输入一个新文档，输出它的主题分布。

LDA之所以有用，就是因为它可以从一篇长长的文档提取少数几个主题，类似于人类整理文件的时候打上标签。这为信息检索提供了便利。

这篇文章会自上而下地介绍LDA：以从NeurIPS论文提取主题为例作为引入，首先将主题模型抽象为一个参数估计问题；然后，引入一些必要的数学工具（如Dirichlet分布、Gibbs采样等）；最后，推导出LDA的训练和测试算法。

👉 这里附上我的LDA代码实现：https://github.com/mistylight/Understanding_the_LDA_Algorithm

一个例子

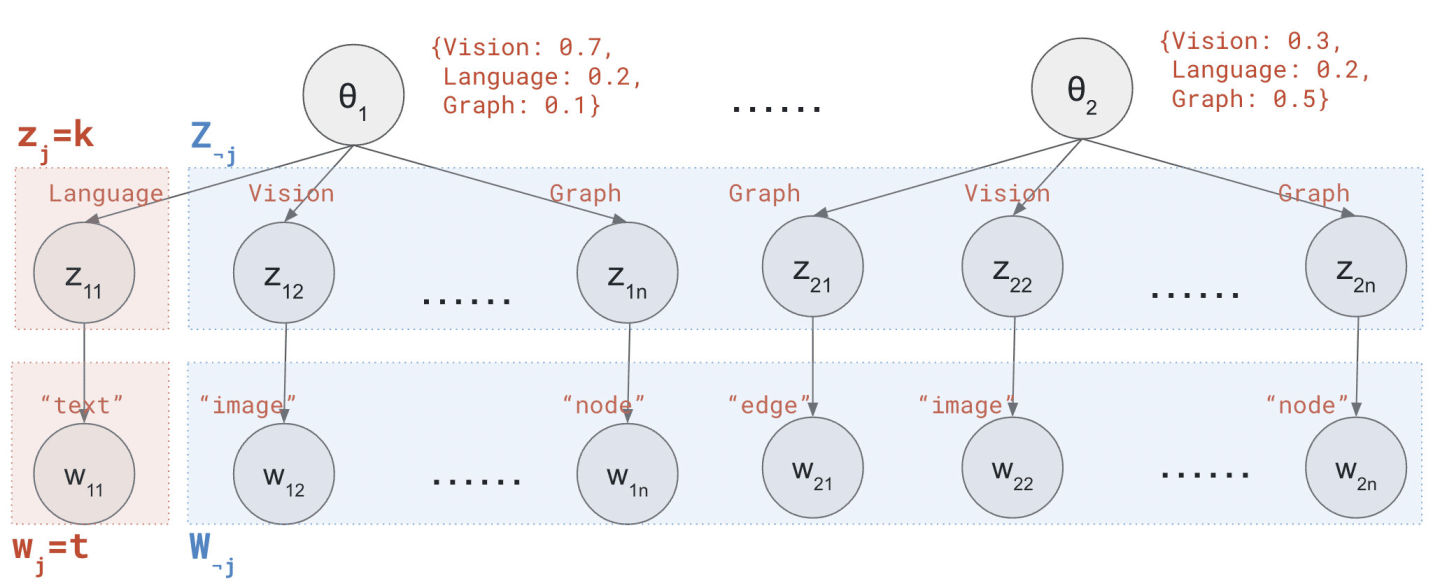
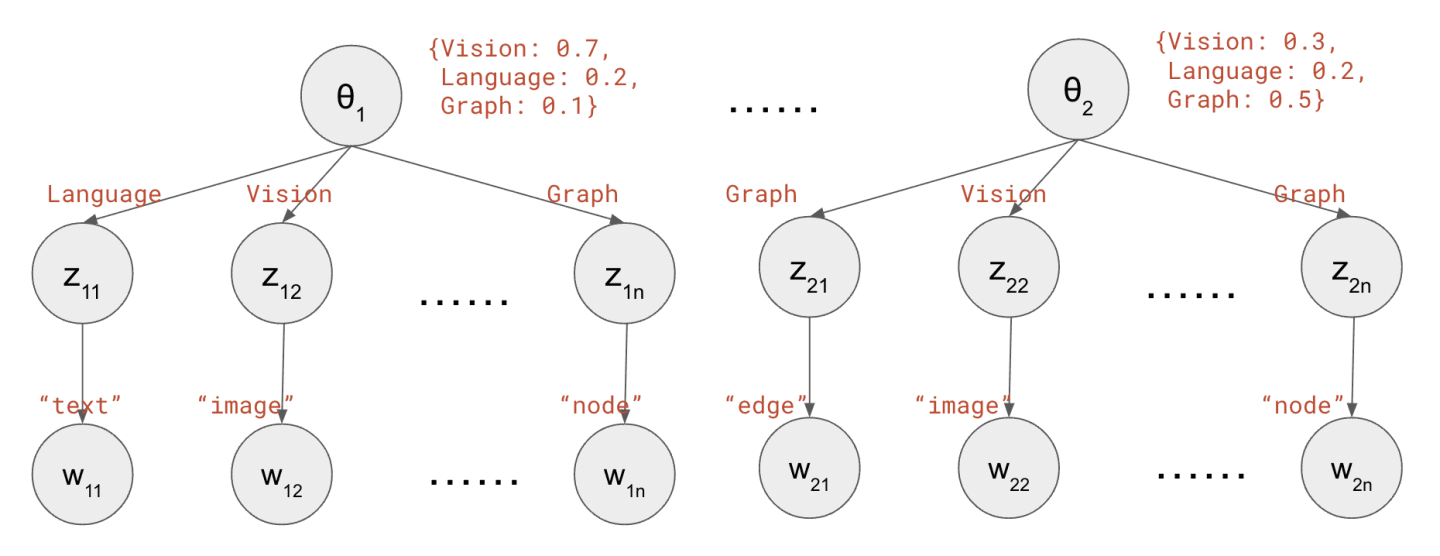
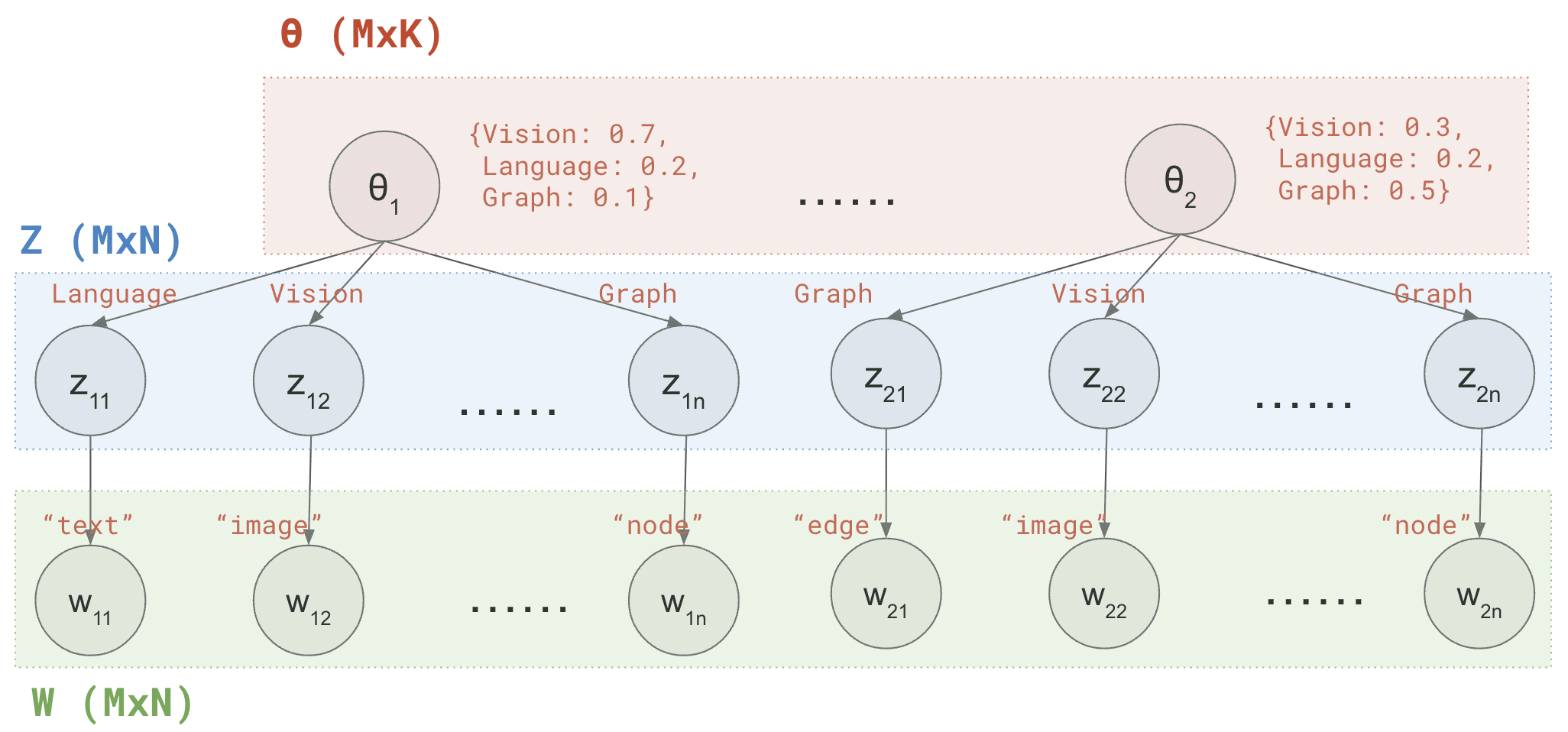
假如，你正在分析一个机器学习会议上发表的论文：有M=1000篇被接受的论文，每篇论文有N=200字的摘要。该会议有K=3个主题：计算机视觉（Vision）、自然语言处理（Language）和图论（Graph）。为了分析每篇论文涉及哪些主题，你做了以下假设：

• 每篇论文都定义了主题的概率分布，e.g.

{Vision: 0.7, Language: 0.2, Graph: 0.1}

• 每个主题都定义了词的概率分布（注意这对所有论文都一样），e.g.

Vision:  {"image":  0.05,  "recognition":  0.01,  "detection":  0.01,  ...}
Language:  {"text":  0.07,  "semantic":  0.02,  "summarization":  0.01,  ...} 
Graph:  {"node":  0.04,  "edge":  0.04,  "clustering":  0.01,  ...}

• 论文中的词语是通过以下程序产生的（如下图所示）。

for m = 1…M // 遍历所有文档

• 随机产生一个主题向量$\vec\theta$, e.g. {Vision: 0.7, Language: 0.2, Speech: 0.1}
• for n = 1…N // 遍历所有单词
  • 根据主题向量$\vec\theta$，随机生成一个主题$z$， e.g. Vision
  • 根据主题$z$，随机生成一个单词$w$，e.g. "image"

在LDA训练时，需要求解以下两个问题：

• 计算M篇论文各自的主题概率分布（$\mathbf \Theta \in \mathbb{R}^{M\times K}$）。
• 计算K个主题各自的词概率分布（$\mathbf \Phi \in \mathbb{R}^{K\times V}$，其中V是单词总数）。

然后就可以在LDA测试时，实现以下目的：

• 给出一篇未见过的新论文，找到它的主题分布（$\vec\theta_{\text{new}}\in \mathbb{R}^K$）。

入门：Dirichlet分布

先验、数据和后验

看一看我们要解决的参数：M个文档中每个文档的主题分布（$\mathbf \Theta$）和K个主题的词分布（$\mathbf \Phi$）。

为了估计它们，LDA算法对它们的先验（prior）进行了一些假设。

什么是先验？它是我们在没有观察到数据的情况下，对参数的信念。

相反，在观察了数据（data）之后，我们会得到后验（posterior）。

通常，我们对后验感兴趣，因为它包含了数据的信息，因此有利于使用MAP（最大后验）或EAP（期望后验）等方法估计参数。

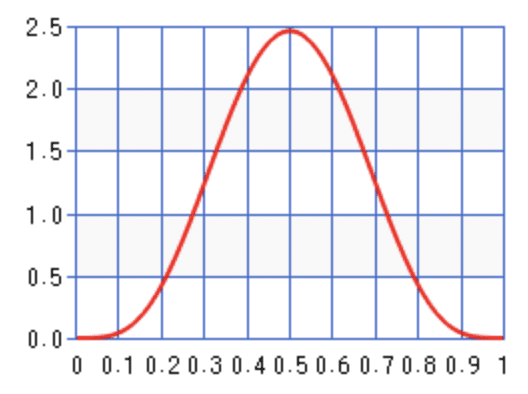
一个例子：假设你有一枚硬币。你认为这是一枚公平的硬币，因此相信，它显示正面的概率很可能在0.5左右（先验$P(p_{\text{coin}})$）。

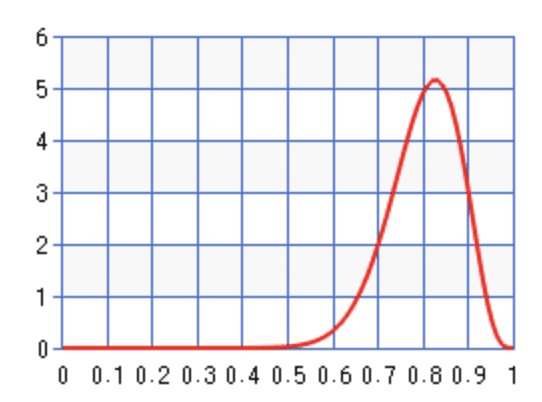
然而，你抛了几次，得到的全是正面（数据 data）。随着证据的积累，你对它显示正面的概率的“信念”会逐渐从0.5变得非常接近于1（后验$P(p_{\text{coin}}\mid \text{data})$）。

在这个例子中，硬币概率的先验和后验，都可以用Beta分布方便地建模。我们可以用后验概率的最大值或平均值来回答：“在观察了几次抛掷后，你认为硬币显示正面的概率是多少？”

一个可能的先验$P(p_{\text{coin}})$	在观测到全是正面后，一个可能的后验$P(p_{\text{coin}}\mid \text{data})$

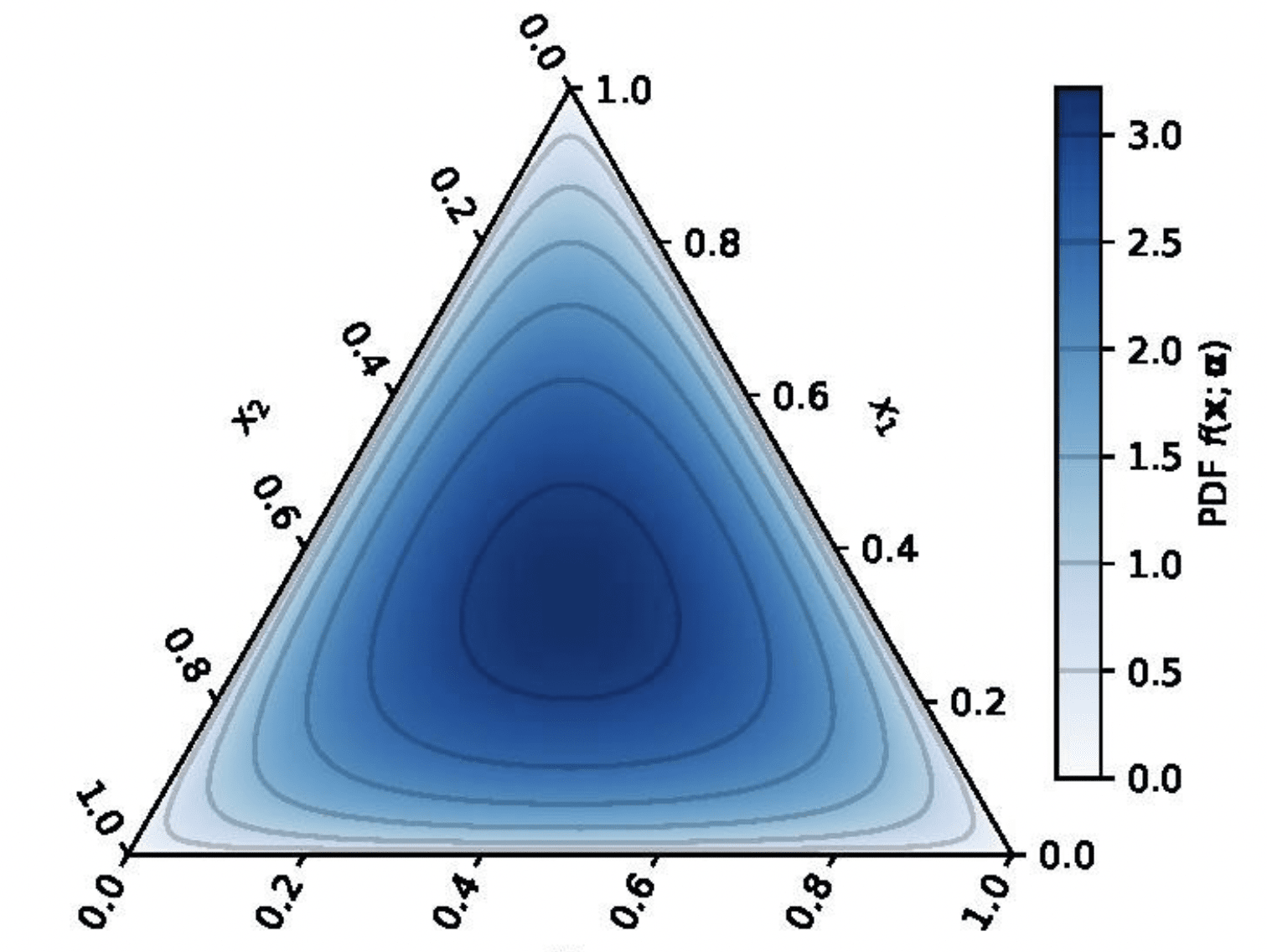
同样，给定一篇论文，在读它之前，我们可能会相信，它的主题分布很可能是对称的，即 {Vision: 1/3, Language: 1/3, Graph: 1/3}（先验$P(\vec\theta)$）。

与硬币类似，你可以把它想象成一个三面的骰子。

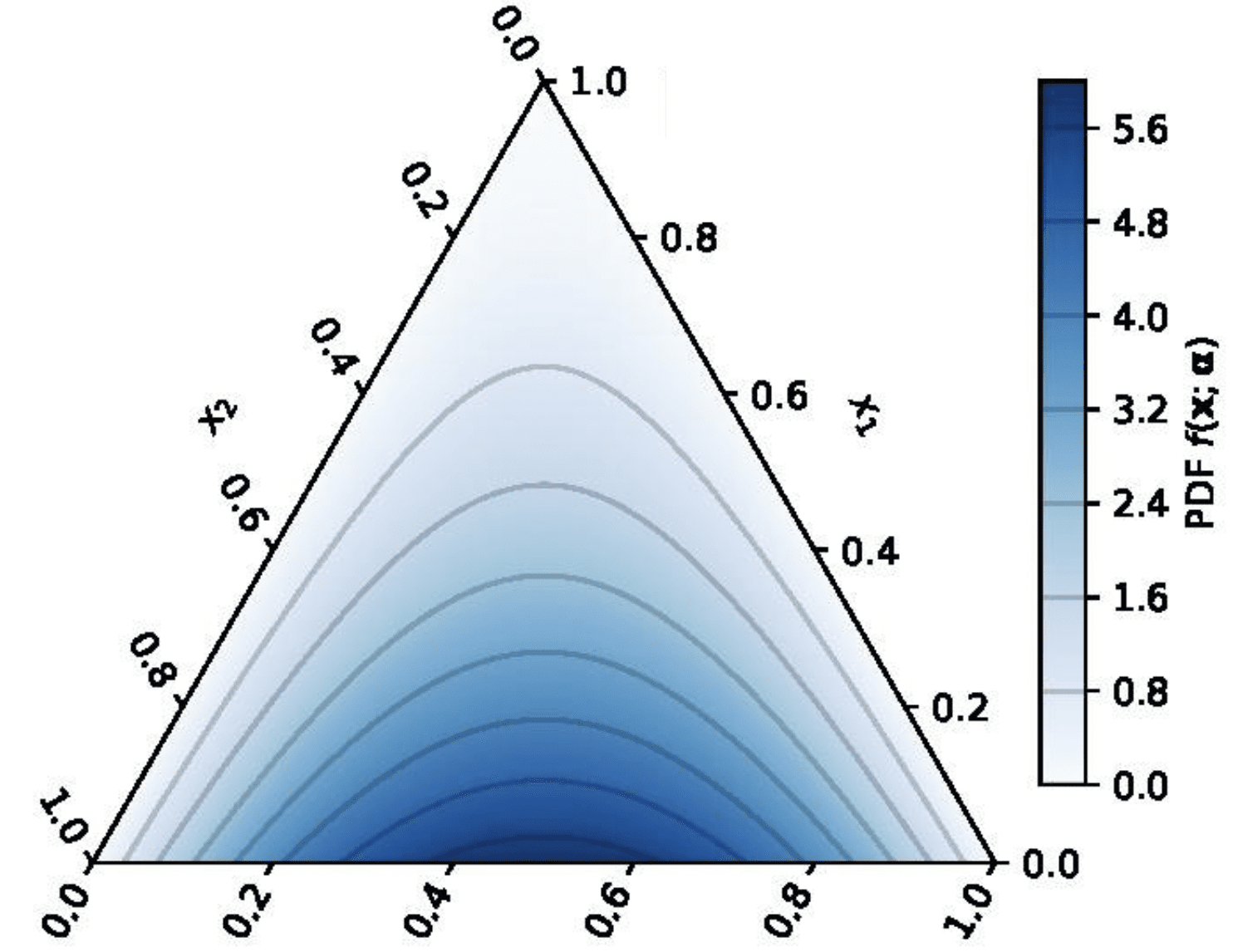
在通读了这篇论文之后，你从来没有遇到过一个关于Graph的词，这意味着在99%的时间里，你看到的是【图像】、【文本】之类的词（数据$\mathbf W$）。

此时，你对其主题比例（骰子各个面的概率）的信念可能会偏移，比如变成 {Vision: 0.5, Language: 0.5, Graph: 0.0}（后验$P(\vec\theta \mid \mathbf{W})$）。

在这个例子中，先验和后验都可以用Dirichlet分布方便地建模。我们也可以用后验概率的最大值或平均值来回答 “在通读这篇论文后，你认为它的主题分布是什么？”

一个可能的先验$P(\vec\theta)$	在观测到全是Vision和Language相关的词后，一个可能的后验$P(\vec\theta\mid \text{data})$
(图片来源)	(图片来源)

注意，在上述两个例子中，Beta/Dirichlet分布并不是我们唯一的选择。

之所以选择它们，主要是因为，它们在数学上很方便：

对于多项/二项分布，如果参数的先验分布是Beta/Dirichlet，那么其后验分布也是Beta/Dirichlet。

这种数学上的便利性，被称为“共轭先验”。

Dirichlet分布：一罐骰子

上文中，我们一直在使用 "信念"这个不严谨的词，来描述以下直觉：

先验/后验是一个概率分布，它们都是对被估计的参数的密概率密度进行建模。

打个比方：一篇论文的主题分布就像一个K面的骰子，那么Dirichlet分布就像一罐骰子。

每次你伸手进去（称之为 “采样”），都会得到一个新的骰子。

在本文的例子中，在你观察数据之前，罐子被认为更可能给你一个公平的骰子；在你观察数据之后，罐子被认为更可能给你一个有偏的骰子。

随着你积累更多的数据，后验的期望值会发生变化。这大致相当于从罐子里多次取样，然后取你得到的骰子的各面概率的平均值，会发现这个平均值在不断地变化。

所以，Dirichlet分布这个“罐子”长啥样呢？

我们记得，这里"骰子"指的是一个多项分布$\text{Mult}(p_1,...,p_n)$，其中$\sum_{i=1}^n p_i=1，p_i \geq 0$。

那么，一罐骰子就是由n个变量$\vec{p} = [p_1,...,p_n]$组成的n元分布。

我们的最终目标，是通过求解后验来估计骰子各个面的概率。

这里有一个重要的问题：用什么做数据呢？

从直观角度讲：一个普通人，想算骰子的概率，一般的做法是抛很多次，然后统计每个面出现的次数。

例如，每篇文档的主题分布可以视作一个3面骰子。你投掷它100次，得到如下结果：

• Vision: 50 (50%)
• Language: 40 (40%)
• Graph: 10 (10%)

而你的先验是，骰子应该是各面等概率的。

将实验数据与你的信念结合的，最简单的方式，是在你的观察中加入一个“伪计数”。

“伪计数”的数量，取决于你的先验有多强。比如，如果你特别相信骰子是各面等概率的，那也许应该加一个较大的伪计数（例如100），这会使后验的期望值更接近于公平的骰子：

• Vision: 50+100 (37.5%)
• Language: 40+100 (35%)
• Graph: 10+100 (27.5%)

否则，应该选择一个很小的伪计数（如1），这会使得估计值更接近于观测数据：

• Vision: 50+1 (49.5%)
• Language: 40+1 (39.8%)
• Graph: 10+1 (10.7%)

幸运的是，Dirichlet分布的数学性质，与这种基于伪计数的直觉，是吻合的。

Dirichlet分布的参数是$\vec{\alpha}=\{\alpha_1,...,\alpha_n\}$，其中每个$\alpha_i$可以被看作是骰子第$i$个结果的伪计数。

我们把Dirichlet分布表示为$\text{Dir}(\vec{p};\vec{\alpha})$，这表示它是一个与骰子概率$\vec{p}$有关的分布，并以伪计数$\vec\alpha$为参数。

它有以下两个很棒的特性：

1. 在观察数据$\vec{x}=[x_1,...,x_n]$($x_i$是第$i$个结果的发生率)之后，Dirichlet后验可以计算为（即，合并伪计数与观测数据）：

   $\text{Dir}(\vec{p}\mid \vec{x}; \vec{\alpha}) = \text{Dir}(\vec{p}; \vec{\alpha}+\vec x)\\$

2. Dirichlet先验的期望值，等于各个$α_i$之间的比率，这使得我们很容易就可以从Dirichlet后验进行参数估计：

   $\mathbb{E}[\text{Dir}(\vec{p}; \vec{\alpha})] = [\dfrac{\alpha_1}{\sum_{i=1}^n \alpha_i}, \dfrac{\alpha_2}{\sum_{i=1}^n \alpha_i},...,\dfrac{\alpha_n}{\sum_{i=1}^n \alpha_i}]\\$

这里，我不打算深挖太多细节，e.g.，Dirichlet分布的具体函数定义，对于其密度函数的若干种直观解释[3]，等等。我个人觉得，如果仅仅是为了了解LDA算法，把它当作是一个“算起来很方便的”数学工具就已经足够了。

Doc-topic和Topic-word骰子

现在回到我们的问题：要估计的参数可以被想象为M个文档-主题骰子（doc-topic dice，各有K个面，$\mathbf{\Theta}\in\mathbb{R}^{M\times K}$ ）和K个主题-词骰子（topic-word dices，各有V个面，$\mathbf{\Phi}\in\mathbb{R}^{K\times V}$）。

M个doc-topic骰子共享同一个先验，而K个topic-word骰子共享另一个先验。

想象一下，有两罐骰子，其中一罐装满了doc-topic骰子，你从中随机抽取M个（$\mathbf{\Theta}=\{\vec{\theta_1},...,\vec{\theta_M}\}$，其中每个$\vec\theta_m$是一个关于主题的K维分布）。这是那M个文档的主题概率分布；

另一个罐子里装满了topic-word骰子，你从中随机抽取K个（$\mathbf{\Phi}=\{\vec{\varphi_1},...,\vec{\varphi_K}\}$，其中每个$\vec\varphi_k$是一个词的V维分布）。这是那K个主题的词概率分布。

我们的目标，是通过求解它们的后验和取期望值，来估计$\mathbf \Theta$和$\mathbf \Phi$的值。

	doc-topic 骰子 Θ	topic-word 骰子 Φ
先验prior	Dir(α)，α为超参数	Dir(β)，β为超参数
数据data	每个主题的单词数（e.g. Vision 100词，Language 200词，Graph 300词）。	同一主题产生的不同单词出现频次（例如，对于主题Vision，“图像”出现10次，“识别”出现20次，等等）。
后验posterior	由LDA计算	由LDA计算

LDA模型

问题抽象

现在，将我们最初的伪代码进行细化，我们可以将LDA生成过程重新总结如下：

// 初始化M个doc-topic骰子和K个topic-word骰子

• for m = 1…M // 遍历所有文档
  • 随机生成一个doc-topic骰子$\vec{\theta_m} \sim \text{Dir}(\vec\alpha)$
    // 这是一个K维的主题概率分布
    // e.g. {Vision: 0.7, Language: 0.2, Speech: 0.1}
• for k = 1…K // 遍历所有主题
  • 随机生成一个topic-word骰子$\vec{\varphi_k} \sim \text{Dir}(\vec\beta)$
    // 这是一个V维的单词概率分布
    // e.g. {"image": 0.05, "recognition": 0.01, "detection": 0.01, ...}

// 生成语料库中所有单词

• for m = 1…M // 遍历所有文档
  • for n = 1…N // 遍历所有单词
    • 随机采样一个主题$z_{mn} \sim \text{Mult}(\vec{\theta_m})$
      // 一个$\{1,...,K\}$之间的整数，代表一个主题，e.g. Vision
    • 随机采样一个单词$w_{mn} \sim \text{Mult}(\vec{\varphi}_{z_{mn}})$
      // 一个$\{1,...,V\}$之间的整数，代表一个单词，e.g. "image"

我们的目标如下：

• LDA训练：对于训练集的文档，从观察到的词$\mathbf{W}$中推断出潜在变量$\mathbf{\Theta}, \mathbf{\Phi}$（即M个doc-topic骰子和K个topic-word骰子），通过计算后验期望值实现（这里，$\vec\alpha, \vec\beta$是超参）：

  $\begin{aligned}\hat{\mathbf{\Theta}} &= \mathbb{E}[P(\mathbf{\Theta} \mid \mathbf{W} ; \vec\alpha, \vec\beta)]\\\hat{\mathbf{\Phi}} &= \mathbb{E}[P(\mathbf{\Phi} \mid \mathbf{W} ; \vec\alpha, \vec\beta)]\end{aligned}\\$

• LDA测试：对于一个新文档，其中单词$\mathbf{W}_{\text{new}}$，推断其潜在变量$\vec\theta_{\text{new}}$。(注意我们为每个文档抽取一个新的doc-topic骰子，但对所有的文档重复使用topic-word骰子。因此，我们只需要推断一个新的$\vec\theta$，而不是$\vec\varphi$）。这可以通过计算后验的期望值来实现:

  $\hat{\vec{\theta_{\text{new}}}} = \mathbb{E}[P(\vec\theta_{\text{new}}\mid \mathbf{W}\cup\mathbf{W_{\text{new}}} ; \vec\alpha, \vec\beta)]\\$

隐变量Z

如何估计$\mathbf\Theta$和$\mathbf\Phi$的后验？还记得我们讨论过，只要我们有数据在手，计算Dirichlet后验是很简单的：

	doc-topic 骰子 Θ	topic-word 骰子 Φ
先验prior	Dir(α)，α为超参数	Dir(β)，β为超参数
数据data	每个主题的单词数（e.g. Vision 100词，Language 200词，Graph 300词）。	同一主题产生的不同单词出现频次（例如，对于主题Vision，“图像”出现10次，“识别”出现20次，等等）。
后验posterior	由LDA计算	由LDA计算

问题是，我们并不真正知道每个词背后的主题是什么！如果你熟悉EM算法，你可能会知道这叫做 “隐藏变量”。

在这里，主题变量$\mathbf Z\in\mathbb{R}^{M\times N}$（M个文档中的N个词各有一个主题），对于计算后验至关重要（见上表），但我们却不知道它的值。

绕过这个难题的一个方法，是在给定单词$\mathbf W \in \mathbb{R}^{M\times N}$的前提下，对$\mathbf Z$的值进行采样：

$\mathbf Z \sim P(\mathbf Z \mid \mathbf W)\\$

这里的直觉是，我们想知道，在看到这些单词的前提下，他们背后最后可能是哪些话题，从而用它们来估计参数也就是最有意义的。

在这里，我们还做了一个近似的处理，即用一个$\mathbf Z$的样本来代表所有可能的$\mathbf Z$的平均情景。这是在有随机成分的神经网络（如VAE）中广泛采用的一种策略。

在数学上，我们可以深入了解为什么从$P(\mathbf Z \mid \mathbf W)$中采样$\mathbf Z$是合理的（参见附录）。

Gibbs采样

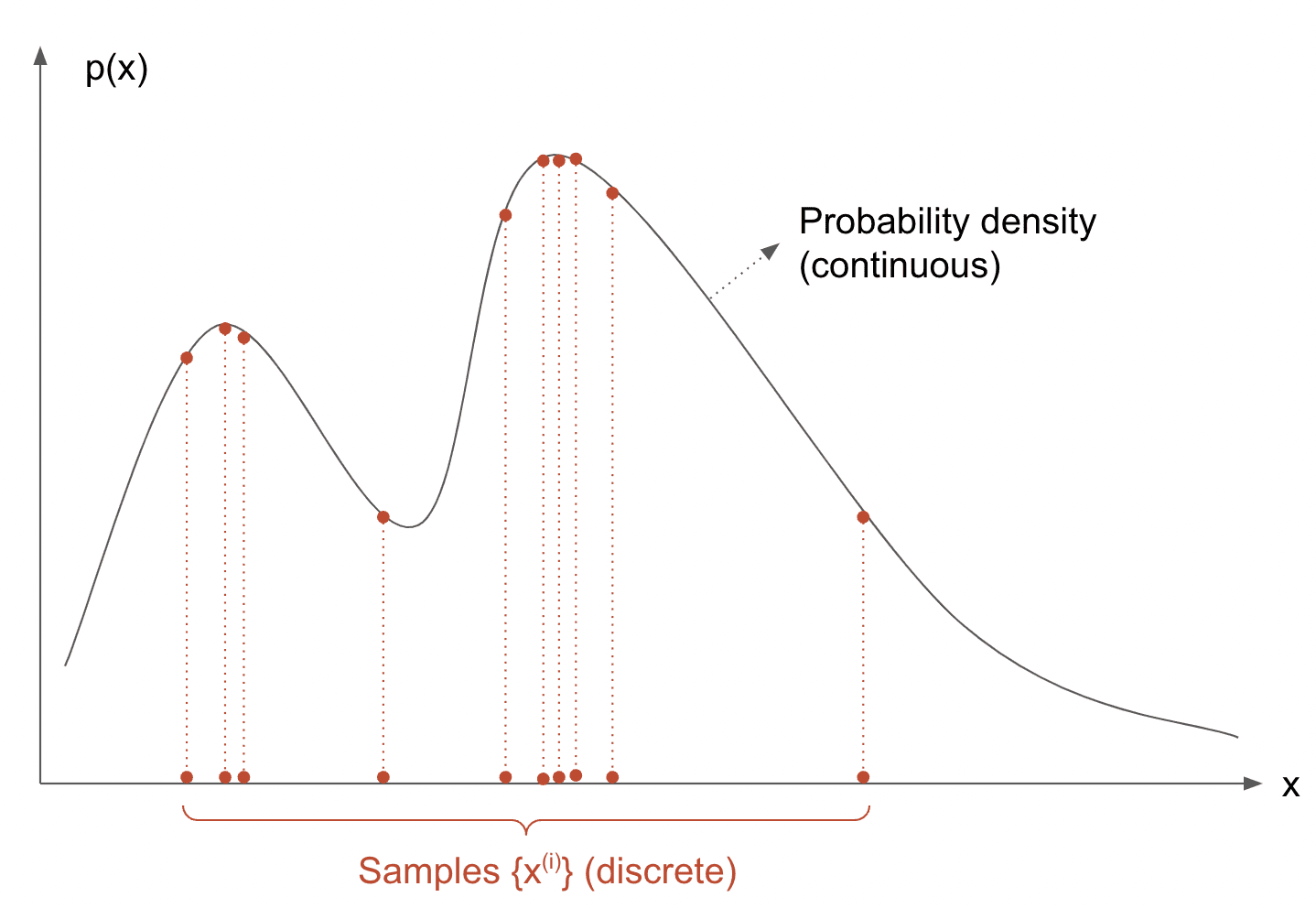
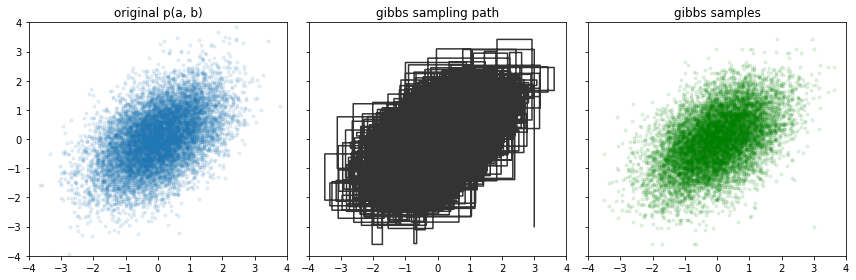
但如何从分布中采样呢？虽然看起来很简单，但这并不是一个简单的问题。尽管如此，有很多高级算法可以实现这一目的。Gibbs采样是我们在这里要使用的算法，因为在LDA的框架下，它的数学推导很方便。我们将在这里直接介绍这个算法，而不解释它的工作原理，感兴趣的读者可以参考这个教程。

图片来源：Jessica Stringham的博客

算法：Gibbs采样

• 输入：$p(\vec x)$的数学表达式。
• 输出：从$p(\vec x)$中采样得到的样本$\{\vec x^{(1)},\vec x^{(2)},...,\vec x^{(T)}\}$。

从一个概率分布中采样。

// 随机初始化$\vec x^{(0)} \in \mathbb{R}^D$

-$[x^{(0)}_1,x_2^{(0)},...,x_D^{(0)}]\leftarrow \text{随机向量}$

// 迭代采样

• for t in 0…T // 重复直至收敛
  • for d in 1…dim($\vec x$): // 遍历$\vec x$的所有维度
    • 采样得到$x^{(t+1)}_d \sim P(\cdot \mid x_1^{(t+1)},...x_{d-1}^{(t+1)},x_{d+1}^{(t)},..,x_D^{(t)}) \quad (*)$
  • 输出$\vec x^{(t+1)}$，作为一个新的样本

用一句话来说，(*)干的事情是：冻结所有其他维度的值，并根据其值对当前维度进行采样。例如，在二维中，Gibbs采样交替进行“冻结y采样x”，以及“冻结x采样y”。

图片来源：Jessica Stringham的博客

而在三维情形中，每次迭代（即内循环）等价于：

$\begin{aligned} x_1^{(t+1)} &\sim P(\cdot \mid x_2^{(t)}, x_3^{(t)}) \quad~~~~~~\text{// freeze }x_2, x_3\text{, only sample }x_1\\ x_2^{(t+1)} &\sim P(\cdot \mid x_1^{(t+1)}, x_3^{(t)})\quad~~~\text{// freeze }x_1, x_3\text{, only sample }x_2\\ x_3^{(t+1)} &\sim P(\cdot \mid x_1^{(t+1)}, x_2^{(t+1)})\quad\text{// freeze }x_1, x_2\text{, only sample }x_3 \end{aligned}$

LDA训练

回顾一下：LDA训练的目标是基于语料库估计$\mathbf \Theta$和$\mathbf \Phi$。

“Doc-topic和Topic-word骰子”一章的分析表明，这需要知道每个主题、每个词的出现频次。

“隐变量Z”一章的分析则表明，为了统计频次，需要知道$\mathbf Z$的值，为此需要对$P(\mathbf Z \mid \mathbf W)$进行采样。

“Gibbs采样”一章则告诉我们，Gibbs采样算法可以帮助我们完成这个采样。

你也许已经注意到了，唯一棘手的部分是(*)行，其含义是“冻结所有其他维度的值，并根据它们的值对当前维度进行采样”。

而对于$\mathbf Z$而言，这意味着 “冻结所有其他词的主题，并对当前词的主题进行采样”。可以写成：

$z_j \sim P(z_j=k\mid\mathbf{Z}_{\neg j}, \mathbf{W})\\$

它的意思是：为了对语料库中第$j$个词的主题进行抽样（我们可以想象，把所有论文的所有词拼在一起，而$j$这个索引遍历其中的所有单词），我们将所有其他词的主题（$\mathbf Z_{\neg j}$）固定。

如果继续推导下去，我们可以得出Gibbs采样的公式为：

$\begin{aligned} &\quad P(z_j=k\mid \mathbf{Z}_{\neg j}, \mathbf{W}) \\ &\textcolor{darkgreen}{\quad\text{\texttt{// 当B被观测到时，P(A|B) ∝ P(A, B) }}}\\ &\propto P(z_j=k, w_j=t \mid \mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j}) \\ &\textcolor{darkgreen}{\quad\text{\texttt{// 对θ和φ积分，计算边缘概率。}}}\\ &= \int_{\vec\theta_m}\int_{\vec\varphi_k} P(z_j=k, w_j=t, \vec\theta_m ,\vec\varphi_k \mid \mathbf{Z}_{\neg j},\mathbf{W}_{\neg j}) d\vec\theta_m d\vec\varphi_k\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 上面这个概率，是以下4个事件的概率的乘积：}}}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 1) 从给定了\(\mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j}\)的Dirichlet后验分布中，采样得到θm}};}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 2) 从θm中，采样得到主题k，概率为θmk;}}}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 3) 从给定了\(\mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j}\)的Dirichlet后验分布中，采样得到φk}};}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 4) 从φk中，采样得到单词t，概率为φkt;}}}\\ &= \int_{\vec\theta_m} \theta_{mk} P(\vec\theta_m\mid \mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j})d\vec{\theta}_m \cdot \int_{\vec\varphi_k} \varphi_{kt}P(\vec\varphi_{k}\mid \mathbf{Z}_{\neg j},\mathbf{W}_{\neg j})d\vec\varphi_k\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 以上两个积分，等价于以下两个期望：}}}\\ &= \mathbb{E}[\theta_{mk} \mid \mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j}] \cdot \mathbb{E}[\varphi_{kt}\mid \mathbf{Z}_{\neg j}, \mathbf{W}_{\neg j}] \\ & \textcolor{darkgreen}{\quad\text{\texttt{// 注意Θ和Φ的后验分布是Dirichlet分布，}}}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 它们的参数是伪计数α, β与观察到的频次的和.}}}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 因此，我们计算M个文档与K个主题之间的共现频次矩阵}}\mathbf{N}_{M\times K,\neg j},}\\ &\textcolor{darkgreen}{\quad\text{\texttt{// 以及K个主题与V个单词之间的共现频次矩阵}}\mathbf{N}_{K\times V,\neg j},}\\ &\textcolor{darkgreen}{\quad \text{\texttt{// 用以计算Dirichlet后验的期望。}}}\\ &\textcolor{darkgreen}{\quad \text{\texttt{// 这里，}}\neg j \text{\texttt{ 下标的意思是，在计算共现频次时，排除了第j个单词。}}}\\ &= \dfrac{\alpha_k+N_{mk, \neg j}}{\sum_{k'} (\alpha_{k'}+N_{mk',\neg j})} \cdot \dfrac{\beta_t+N_{kt,\neg j}}{\sum_{t'}(\beta_{t'}+N_{kt',\neg j})} \quad (**) \end{aligned}$

这里的数学比较密集，但含义却很直观：

重复以下步骤直至收敛：对语料库中的每个词，排除它，计算doc-topic和topic-word的共现频次，然后根据（**）重新对当前词的主题进行采样。

最后，由Gibbs采样产生的变量$\mathbf Z$的值序列，就是$P(\mathbf Z \mid \mathbf W)$的样本。

为了估计$\mathbf \Theta$和$\mathbf\Phi$，我们可以取多个样本的平均值，也可以只用一个样本进行近似。

如果我们只用一个样本，那么通过对Dirichlet后验计算期望，可以得到$\hat{\mathbf\Theta}, \hat{\mathbf{\Phi}}$的估计值为：

$\begin{aligned} \theta_{mk} &= \dfrac{\alpha_k+N_{mk}}{\sum_{k'} (\alpha_{k'}+N_{mk'}) } \\ \varphi_{kt} &= \dfrac{\beta_t+N_{kt}}{\sum_{t'} (\beta_{t'}+N_{kt'})} \end{aligned} \\$

这里，在采样之后，$N_{mk}$指的是文档m中具有主题k的词的数量；$N_{kt}$指的是整个语料库中词t和主题k之间的共现次数。直观上，对于$\mathbf\Theta$，我们将伪计数$\vec\alpha$与观察到的doc-topic共现频次相结合；对于$\mathbf\Phi$，我们将伪计数$\vec\beta$与观察到的topic-word共现频次相结合。

我们也可以选择采取多个$\mathbf Z$的样本，用它们来分别估计$\mathbf \Theta$和$\mathbf\Phi$，并在多个样本之间取平均值。这将需要更多的计算资源，但可以得到一个更不偏的估计。

LDA测试

LDA测试的目的是在给定一个新文档的情况下估计$\vec\theta_{\text{new}}$的主题分布。与LDA训练相比，唯一的区别是现在的观测量变成了$\mathbf W+\mathbf W_{\text{new}}$，而我们需要做的是对新文档中的每个词进行主题抽样。

因此，Gibbs采样公式变成了：

$\begin{aligned} &\quad P(z_j=k\mid \mathbf{Z}_{\neg j}, \mathbf{W}+\mathbf{W}_{\text {new}}) \\ &\propto P(z_j=k, w_j=t \mid \mathbf{Z}_{\neg j}, \mathbf{W},\mathbf{W_{\text{new}, \neg j}}) \\ &= \dfrac{\alpha_k+N_{k, \neg j}}{\sum_{k'} (\alpha_{k'}+N_{k',\neg j})} \cdot \dfrac{\beta_t+N_{kt}+N_{\text{new},kt, \neg j}}{\sum_{t'}(\beta_{t'}+N_{kt'}+N_{\text{new},kt',\neg j})} \quad (***) \end{aligned}\\$

其中，$N_{k,\neg j}$指的是新文档中主题为k的词的数量（不包括第j个词），而$N_{\text{new},kt,\neg j}$指的是新文档中词t与主题k的共频次（不包括第j个词）。

最终，得到$\vec\theta_{\text{new}}$的估计：

$\theta_{\text{new},k} = \dfrac{\alpha_k+N_k}{\sum_{k'}(\alpha_{k'}+N_{k'})} \\$

其中，$N_k$指的是在完成了主题抽样之后，新文档中具有主题k的词的数量。

代码实例：NeurIPS（19xx-20xx）中的主题变迁

本节将使用一个实际的例子（NeurIPS论文）来演示LDA训练和测试的使用。

代码在这里 👉 https://github.com/mistylight/Understanding_the_LDA_Algorithm

数据

我使用的，是来自Kaggle上的NeurIPS论文数据集，其中包含1987年至2016年期间被NeurIPS接收的论文内容。我们分别选择最早的1000篇论文和最新的1000篇论文，用它们训练两个独立的LDA模型。

我对一个问题特别感兴趣：在大约30年的时间里，NeurIPS的主题是如何转变的？

对于每篇论文，我保留摘要中的前200个词，并将总词汇量限制在10000个。我将主题的数量设定为K=10，因为我觉得NeurIPS的主题会有一定多样性，但不会太多。

LDA训练

在这里，我将展示主题词骰子$\mathbf\Phi$的结果，因为它通常是我们比较感兴趣的 —— 语料库中存在哪些主题？每个话题是什么样子的？

19xx年的论文

下面是最早的1000篇论文（换句话说，它们是在20世纪发表的）的10个主题和它们概率最大的10个词。颜色越深，该词在相应的主题中的权重越大：

我们可以粗略地看出大多数主题所对应的内容（注意，这种解释完全是主观的！）。

• 主题0：训练机器学习模型
• 主题1：数学符号/电路设计
• 主题2：信号处理
• 主题3：强化学习
• 主题4：神经网络
• 主题5：核方法
• 主题6：语音识别
• 主题7：神经网络的生物学灵感
• 主题8：计算机视觉
• 主题9：概率论/贝叶斯网络

20xx年的论文

以下是最新的1000篇论文（发表于2016年前后）的10个主题和它们概率最大的前10个词：

而我们也可以尝试解释每个主题的含义，然而这次我们无法得到非常好的解释：

• 主题0：训练深度神经网络
• 主题1：一般机器学习
• 主题2：（？）
• 主题3：生成模型（GAN/VAE）
• 主题4：神经网络
• 主题5：（？）
• 主题6：（？）
• 主题7：强化学习
• 主题8：图论
• 主题9：计算机视觉

有趣的是，有些主题在30年后仍然很火，例如强化学习和计算机视觉；有些主题不像以前那么火了，例如核方法；最后，有些主题近年来变得越来越火，例如图论。

LDA测试

给定一篇新论文，LDA测试旨在找到其主题分布。

在这里，我将用在19xx年论文上训练的LDA模型，去预测一篇未用于训练的19xx年论文的主题：

Title: Decomposition of Reinforcement Learning for Admission Control
Abstract: This paper presents predictive gain scheduling, a technique for simplifying reinforcement learning problems by decomposition. Link admission
control of self-similar call traffic is used to demonstrate the technique.
The control problem is decomposed into on-line prediction of near-future call arrival rates, and precomputation of policies for Poisson call arrival processes. At decision time, the predictions are used to select among the policies. Simulations show that this technique results in significantly faster learning without any performance loss, compared to a reinforcement learning controller that does not decompose the problem.

以下是模型预测的主题（回忆一下，这是$\vec\theta_{\text{new}}$）：

[0.1299, 0.0005, 0.0005, 0.6124, 0.0005, 0.0005, 0.2144, 0.0403, 0.0005, 0.0005]

其中，每个数字对应于一个主题。最高的主题是主题3（权重为60%以上），这与我们的直觉一致，即这篇论文与强化学习高度相关。

结语

当我在大三开始学习LDA算法的时候，我选择了最著名、最全面的中文LDA教程——《LDA数学八卦》[3] 作为入门读物。如果你纯粹对数学感兴趣，而且完全不需要赶时间将LDA应用到你的项目中的话，那么这是一本非常好的教程。然而，虽然我很感激这份教程没有假设读者具有统计机器学习知识，也非常清晰地解释了算法的每一个组成部分，我还是很快地迷失在了大量本可以作为黑箱子一笔带过的细节与证明之中。追踪所有的变量与它们的上下文令我感到十分吃力，以至于当我第一次读它时，基本完全没看懂。我需要经常前后翻看，以回答我脑海中涌现的大量问题——phi是什么？为什么要对Z进行采样以估计Phi？等等，Z又是什么？诸如此类。我相信这种挣扎并不仅有我一个人曾经经历过，而这也成为了我写这篇文章的动机。

我认为，如果教程是以自下而上的方式编写，那么这些问题是不可避免的。这就像在开始时显示每一个像素，然后逐渐缩小以显示整张图片一样。我尝试做相反的事情 —— 在开始时展示图片，然后逐渐放大至每一个像素。缺点是，我不能像《LDA数学八卦》那样深入而严谨地研究数学，而这也许会让一些读者不满意。尽管如此，我希望它能对工程师更加友好，特别是对于那些像当年的我一样，需要理解算法的直觉，却又没有太多时间也没有太大必要去研究所有细节的人。

参考文献

[1] Latent Dirichlet Allocation. David M. Blei, Andrew Y. Ng, Michael I. Jordan. 2003. https://www.jmlr.org/papers/volume3/blei03a/blei03a.pdf

[2] Parameter estimation for text analysis. Gregor Heinrich. 2005. http://www.arbylon.net/publications/text-est.pdf

[3] LDA数学八卦. 靳志辉. 2013. https://bloglxm.oss-cn-beijing.aliyuncs.com/lda-LDA%E6%95%B0%E5%AD%A6%E5%85%AB%E5%8D%A6.pdf