Misty Light

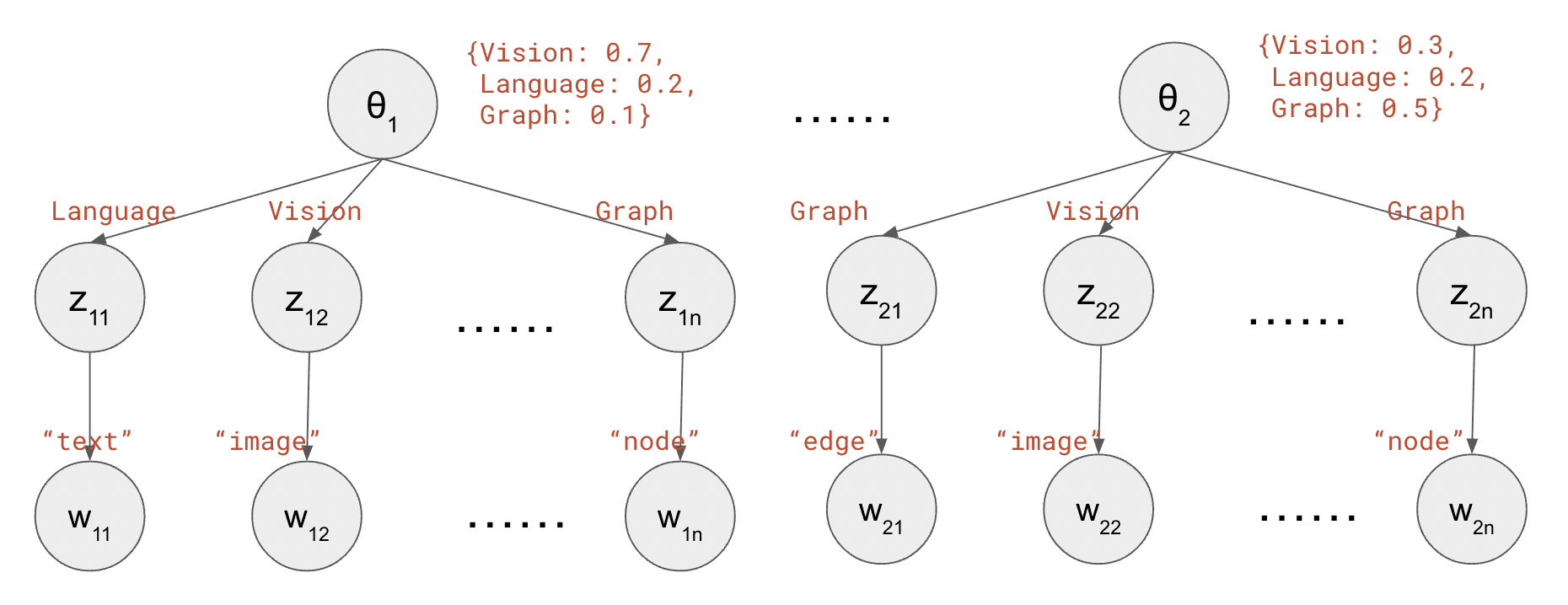
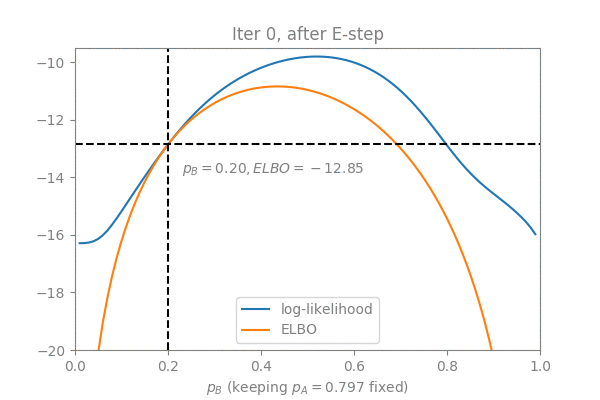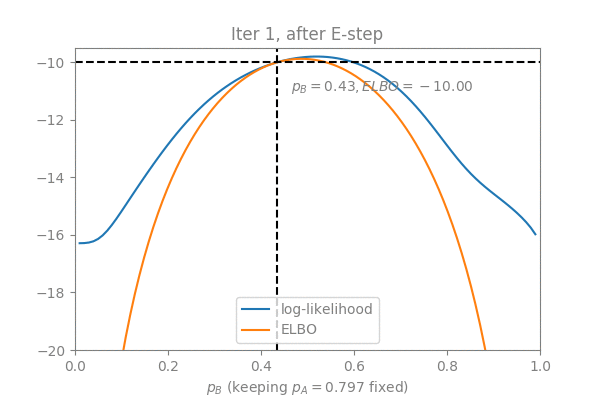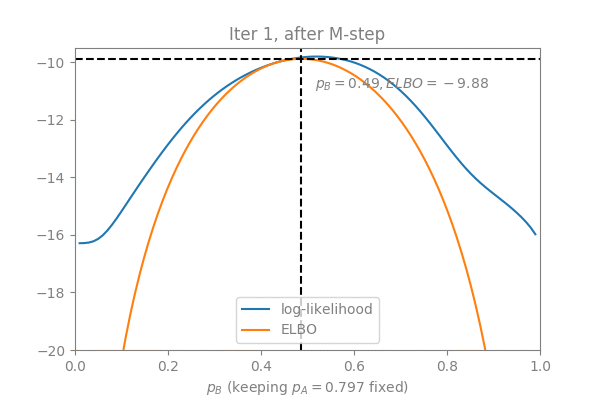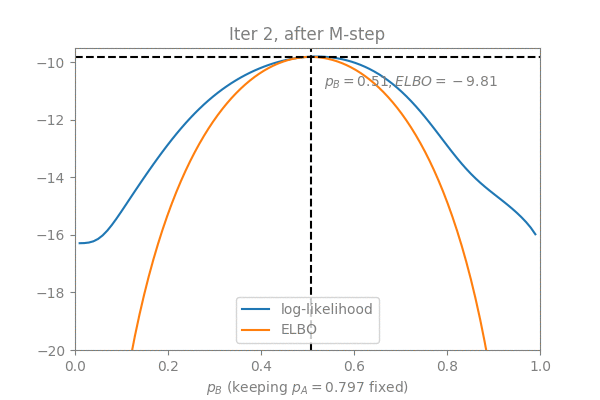
The Latent Dirichlet Allocation (LDA) algorithm is a text mining algorithm that aims to extract topics from long texts. In a nutshell, LDA assumes that each document defines a distribution over topics, and each topic defines a distribution over words. Each word is generated by first sampling a topic from the document, and then sampling a word from the topic. To train an LDA is to solve for the parameters of these two distributions (doc-topic and topic-word) given many documents; To evaluate an LDA usually means predicting the topic distribution for a new unseen document.

This article focuses on the math behind VAE (variational autoencoder). Are you also confused by the coexistence between the simple neural net implementation and the complicated math behind it? Why are these two drastically different things interrelated? If so, this article is likely for you. My VAE implentation can be found at: https://github.com/mistylight/Understanding_the_VAE_Model

The EM algorithm is very straightforward to understand with one or two proof-of-concept examples. However, if you really want to understand how it works, it may take a while to walk through the math. The purpose of this article is to establish a good intuition for you, while also provide the mathematical proofs for interested readers. The codes for all the examples mentioned in this article can be found at https://github.com/mistylight/Understanding_the_EM_Algorithm.

In the previous post, we case studied two examples: two coins and GMM, provided the algorithms for solving them (without proof), and derived a generalized form of the EM algorithm for solving a family of similar problems — finding the maximum log-likelihood with unknown hidden variables. This post will focus on the proof: Why are the algorithms showcased in the two examples mathematically equivalent to the final form of EM?